This one article discusses two Machine Learning methods. They are Decision Tree (also known as Classification and Regression Tree) and later Random Forest. Decision tree, as its name suggests, takes the form of tree to decide which classification new observations are in. Mostly, we actually have used this decision tree method in daily life to decide things. If A happens, then do B. Or else, do C. This Decision Tree in Machine Learning will build a Decision Tree according to the data user feeds to the model. If you are not familiar with Machine Learning basic, please find an article discussing it here. After that, come back here to this article again.
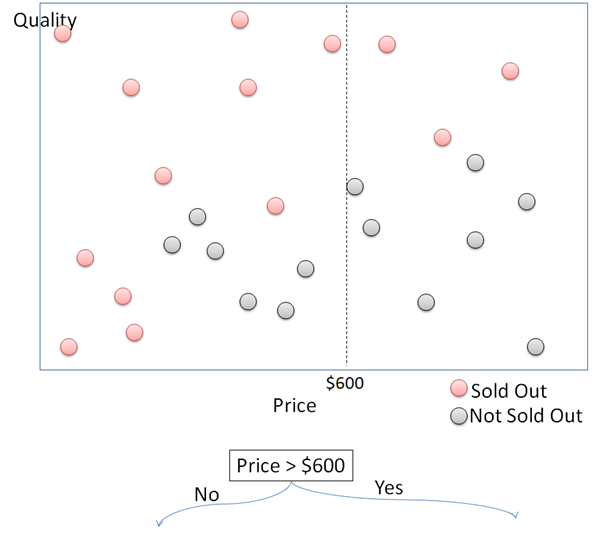
How Decision Tree works in simple way is expressed using the following data. This plot shows purchased goods plotted for their price in x axis and quality in y axis. The purchased goods are then divided into “sold out” and “not sold out”. This article will try to build a Decision Tree to detect whether a thing will be sold out or not according to its price and quality.

First, split the data points into two divisions by the price. Data points with price higher and lower than $600 are divided into right and left. For each of the side, split the data points again into 2 parts according to the quality. For data points with price above $600, they will be sold out if the quality is above 60, and not sold out if the quality is under 60. This process continues to divide those data points while growing the Decision Tree.

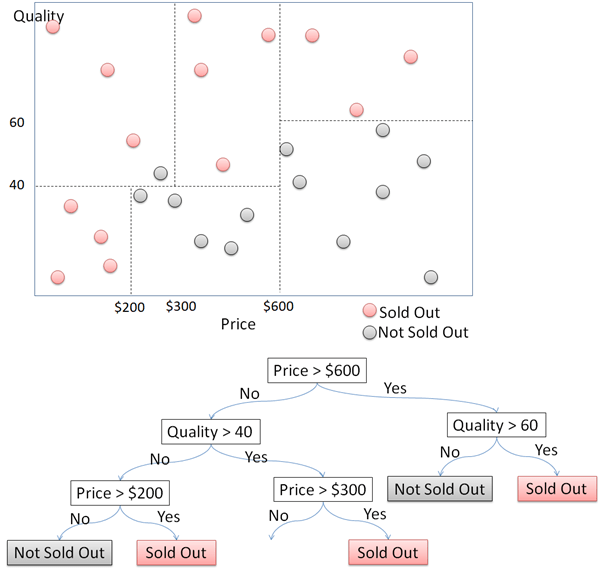

The example above illustrate growing Decision Tree in simple way as the data points only have 2 dimensions. Things will be more complicated if the data has more than 3 dimensions or parameters. To practice this, we will use Hotel Customer Data. The data is dummy data I created. The data contains the information of customers opinion of a hotel. There are 500 observations or rows in this data frame. Each observation represents one customer. There are 12 variables, with data structure as following.
>str(CustomerData)
data.frame': 500 obs. of 12 variables:
$ Id : int 1 2 3 4 5 6 7 8 9 10 ...
$ Gender : Factor w/ 2 levels "Female","Male": 1 1 1 2 2 2 2 1 2 2 ...
$ Age : num 33 30 37 34 33 34 35 30 39 34 ...
$ Purpose : Factor w/ 2 levels "Business","Personal": 2 2 2 2 2 2 2 2 1 2 ...
$ RoomType : Factor w/ 3 levels "Double","Family",..: 1 2 3 1 1 1 1 2 1 1 ...
$ Food : num 21 32 46 72 84 67 56 10 73 97 ...
$ Bed : num 53 32 25 30 7 46 0 19 12 30 ...
$ Bathroom : num 24 18 29 15 43 16 0 1 62 26 ...
$ Cleanness : num 44 44 20 55 78 61 9 53 65 59 ...
$ Service : num 46 74 24 38 51 44 32 58 56 46 ...
$ Satisfaction: Factor w/ 3 levels "Dissatisfied",..: 1 1 1 1 2 2 1 1 2 2 ...
$ Repeat : Factor w/ 2 levels "No","Repeat": 2 1 1 2 2 1 1 2 2 1 ...

Customers are requested to fill a survey form to score 5 parameters of the hotel and finally give an overall satisfaction conclusion. The 5 parameters are food, bed, bathroom, cleanness, and service. The five parameters are scored in numeric from 0 to 100. 0 represents very bad and 100 represents very good. The overall satisfaction asks the customer to fill one from three classes, satisfied, neutral, or dissatisfied. There are other variables, like age, purpose, room type, and repeat, but they are not discussed in this article.

The script below will grow a Decision Tree using 3 parameters of hotel customers: gender, purpose, and room type to classify customers overall satisfaction. The three parameters are in categorical format. The satisfaction classification is expressed in 3 classes. They are “satisfied”, “neutral”, and “dissatisfied”.
# Load the rpart package
library(rpart)
# Build a model to predict according to selected parameters. Here we try categorical parameters
TreeModel <- rpart(Satisfaction~Gender+ Purpose + RoomType, data = trainCustomer, method = "class", control = rpart.control(cp = 0))
# predict the test data
predictTree <- predict(TreeModel, testCustomer, type = "class")
# Load the rpart.plot package
library(rpart.plot)
# visualize the decision tree
rpart.plot(TreeModel, tweak = 1.5)

> # percentage of accuracy
> table(predictTree, testCustomer$Satisfaction)
predictTree Dissatisfied Neutral Satisfied
Dissatisfied 16 16 8
Neutral 15 24 21
Satisfied 0 0 0
> mean(predictTree == testCustomer$Satisfaction)
[1] 0.4
The accuracy is very low, only 40%. Now, the Decision Tree script will be run again. This time all of the parameters or predictors will be used. The model later will decided itself which parameters are most significant to grow the Decision Tree. It even cannot predict “Satisfied”.
# Create decision tree model using all of the parameters
TreeModel2 <- rpart(Satisfaction ~ ., data = trainCustomer, method = "class", control = rpart.control(cp = 0))
# predict the test data
predictTree2 <- predict(TreeModel2, testCustomer, type = "class")
# visualize the decision tree
rpart.plot(TreeModel2, tweak = 1.3)
head(data.frame(testCustomer[,c(6:9, 11)],predictTree2), 20)
The second Decision Tree here has high accuracy of 89% in classifying the customer overall satisfaction. It takes “bathroom”, “cleanness, “bed”, and “food” s its predictors. Find the generated Decision Tree below.

> # percentage of accuracy
> mean(predictTree2 == testCustomer$Satisfaction)
[1] 0.89
> table(predictTree2, testCustomer$Satisfaction)
predictTree2 Dissatisfied Neutral Satisfied
Dissatisfied 26 4 0
Neutral 4 36 2
Satisfied 1 0 27
Here is the classification result of the first 20 observations of the test data.
Food Bed Bathroom Cleanness Satisfaction predictTree2
488 42 64 68 40 Neutral Neutral
158 100 37 25 59 Neutral Neutral
126 55 80 93 84 Satisfied Satisfied
113 100 87 63 72 Satisfied Neutral
325 58 32 0 19 Dissatisfied Dissatisfied
421 82 100 70 83 Satisfied Satisfied
154 82 45 10 99 Neutral Neutral
481 92 89 86 100 Satisfied Satisfied
253 15 70 38 0 Dissatisfied Dissatisfied
460 28 51 84 20 Neutral Neutral
64 23 33 29 86 Neutral Dissatisfied
373 51 69 53 78 Neutral Neutral
89 67 46 16 61 Neutral Neutral
402 25 36 11 23 Dissatisfied Dissatisfied
252 42 60 90 12 Neutral Neutral
406 45 40 14 32 Dissatisfied Dissatisfied
67 83 61 15 79 Neutral Neutral
128 89 86 100 100 Satisfied Satisfied
280 94 52 90 72 Satisfied Satisfied
392 34 38 5 8 Dissatisfied Dissatisfied
The created Decision Tree above has depth of 4. Now, examine the script below that build another Decision Tree model using the argument maxdepth = 3. This limits the maximum depth of the Decision Tree to be 3. We can see that by cutting the overgrown branch can actually increase the accuracy. The accuracy of the third Decision Tree we have is 91%. The Decision Tree now is also more simple than the previous one.
# Tend to of overgrown tree
# set the maxdepth of 3 for the tree
TreeModel3 <- rpart(Satisfaction ~ ., data = trainCustomer, method = "class", control = rpart.control(cp = 0, maxdepth = 3))
# Predict the test data
predictTree3 <- predict(TreeModel3, testCustomer, type = "class")
# plot the decision tree
rpart.plot(TreeModel3, tweak = 1.3)
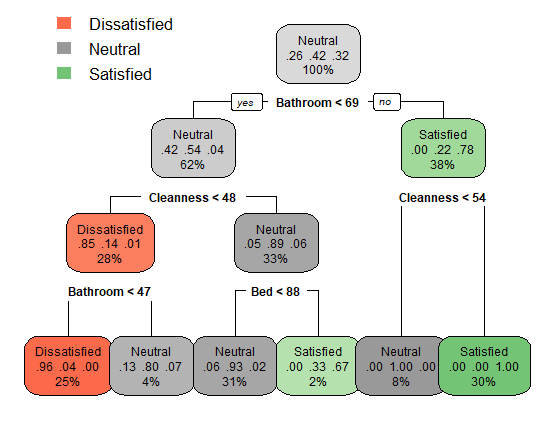
> # Compute the accuracy of the simpler tree
> mean(predictTree3 == testCustomer$Satisfaction)
[1] 0.91
> table(predictTree3, testCustomer$Satisfaction)
predictTree3 Dissatisfied Neutral Satisfied
Dissatisfied 25 1 0
Neutral 5 39 2
Satisfied 1 0 27
Another way to make the Decision Tree to be more simple is pruning. After the Decision Tree is grown, it can be seen as too complicated. Pruning can be applied to reduce less important branches of the Decision Tree so that it is less complicated. Cutting the less important branches is done at the least complex point where relative error does not decrease significantly anymore. The plot below shows the relative error in y-axis and cp in x-axis representing the complexity. The relative error drops when The Decision Tree gets more complex, or cp approaches 0. Figure out that c = 0.024 is the point where relative error does not decrease significantly anymore if the the cp is reduced.
# Examine the complexity plot
plotcp(TreeModel3)
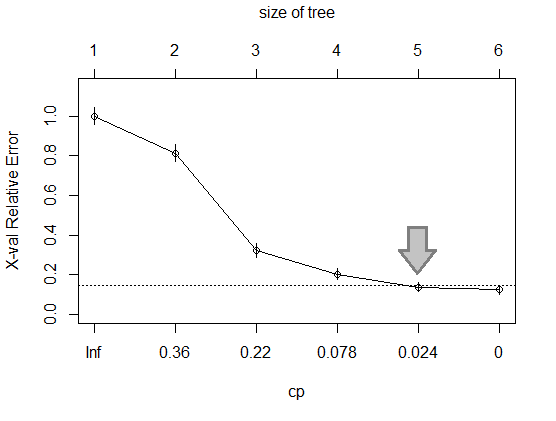
# Prune the tree
TreeModel3_pruned <- prune(TreeModel3, cp = 0.024 )
rpart.plot(TreeModel3_pruned)
# Predict the test data
predictTree3_pruned <- predict(TreeModel3_pruned, testCustomer, type = "class")
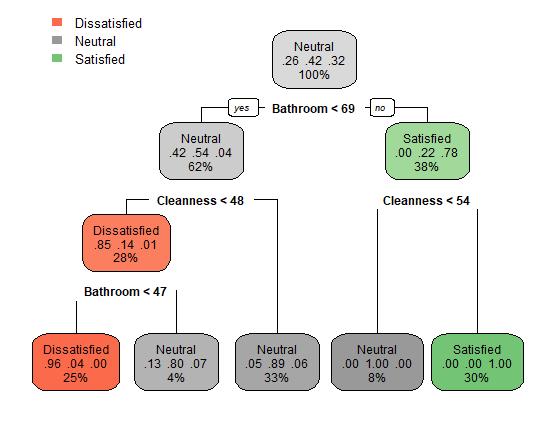
Here is the result and accuracy of the Decision Tree model after pruned with cp = 0.024.
> mean(predictTree3_pruned == testCustomer$Satisfaction)
[1] 0.9
> table(predictTree3_pruned, testCustomer$Satisfaction)
predictTree3_pruned Dissatisfied Neutral Satisfied
Dissatisfied 25 1 0
Neutral 6 39 3
Satisfied 0 0 26
Now, we will discuss another Machine Learning method which still related to the Decision Tree. It is called Random Forest. The Random Forest model creates a number of different Decision Trees using the same data. When the test data are input into the Random Forest model, all of the Decision Trees will classify the test data. After that, the Decision Trees will vote which classification the test data are in.
The picture below illustrates Random Forest which is composed of a number of Decision Trees. Each Decision Tree classifies test data into class “A” and “B”. Since there are more Decision Trees that classifies the test data into “A”, it is decided that the test data is classified into “A” class.

The script below tries to classify the hotel customer satisfaction using Random Forest method.
> mean(PredictRF == testCustomer$Satisfaction)
[1] 0.97
> table(PredictRF, testCustomer$Satisfaction)
PredictRF Dissatisfied Neutral Satisfied
Dissatisfied 29 0 0
Neutral 2 40 1
Satisfied 0 0 28


2 thoughts on “Decision Tree/Classification and Regression Tree and Random Forest”